Artificial Neuron

What is a Neural Network? Quite obvious: it is a Network made of artificial neurons. Artificial neurons are simple, small bricks that allow us to develop big neural buildings.

Here I will show you a depiction of the artificial Neurons and of the Neural Network that I find useful when I want to have a practical representation of what a Neural Network is. It is important to notice and I prefer to note it since the beginning that this representation is just "educational", do not focus on it too much: I will show immediately after that this representation can be easily expressed as matrix product.

The neuron

The input of an artificial neuron is an array of real numbers (let‘s suppose that the input is an array of \(n\) elements). Each input item (ie any element of our input array) is multiplied for a correspondent weight (so that each neuron keeps track of an array which has again \(n\) elements) and all this products are summed together. Additionally a constant (usually called bias) is added to the previous sum. The result of these operations is then passed through a function, usually called activation function (different functions can be used, depending on the type of the neuron). That is all: an artificial neuron performs the weighted sum of its inputs, it adds an additional constant and then it puts the result of this sum into an activation function, the output of this function is the output of the neuron itself.

The image below shows graphically the operations performed by an artificial neuron (the activation function used here is the identity function \(y(x) = x\) which is a perfectly valid activation function, although it does not change at all the result of the previous sum):

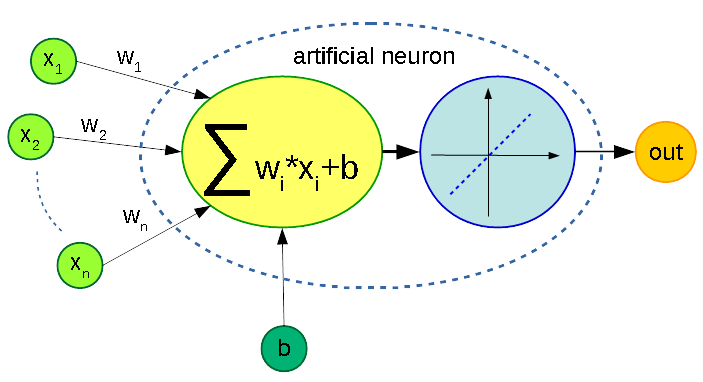
Input is the array \((x_1, \dots, x_n)\) and it is shown in light green, the bias is \(b\) (dark green) and it is quite common to see it as an additional (unweighted) input of the neuron, the yellow oval represent the weighted adder, the blue oval the activation function, the final output is orange.

Layers

To build Neural Networks, neurons are organized in layers just as the bricks within a wall. Each neuron of the layer operates on an input array that is simply the output of the previous layer. The actual input of the network can be seen just as the output of a fake layer.

Now let‘s keep track of some dimensions. Suppose that the input has a size of \(n\) (an array with \(n\) elements). Each neuron in the first layer has an equal number of weights (\(n\) weights for each neuron). Suppose that we have \(m\) neurons in the first layer, the output of the first layer will be an array with \(m\) elements. So that each neuron in the second layer will have \(m\) weights. And so on.

The number of weights of each neuron of a layer is equal to the number of inputs of the layer and the number of outputs of each layer is equal to the number of neurons of that layer. Pretty simple, isn‘t it?

The following picture shows a simple network made by 3 layers (in the first 2 layers there are 4 neurons each and in the third layer there are 2 neurons):

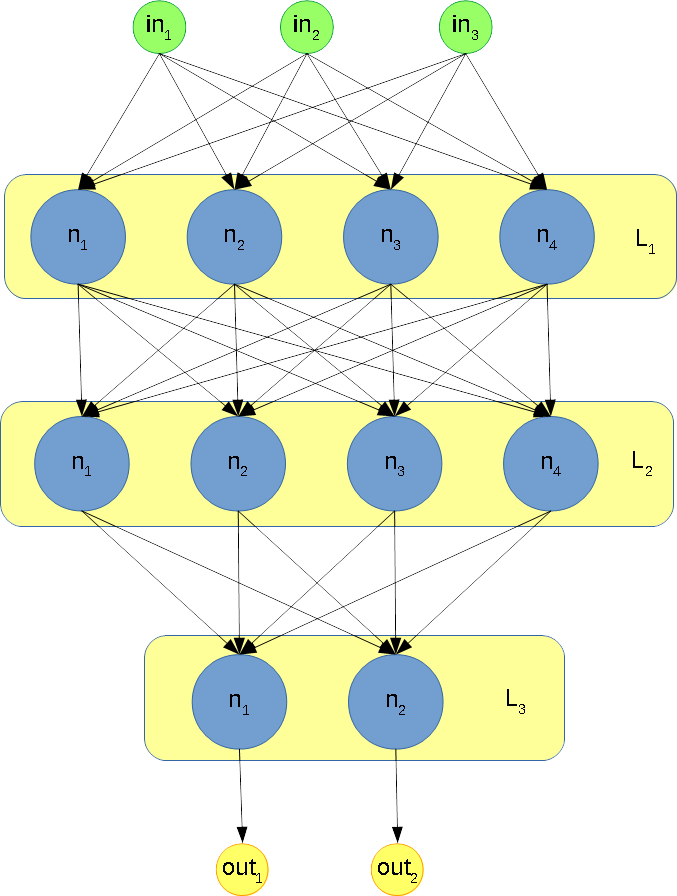
A layer of neuron is a matrix

Now we have a picture of what a Neural Network is. Let‘s forget it for a more suitable mathematical form!

Here I will consider a single layer of our network depiction. Suppose, as usual, that our input is an array of \(n\) elements or, even better a matrix with 1 rows and \(n\) columns. Now suppose that our layer has \(m\) neurons. As explained above each neuron of the layer will have \(n\) weights. Now we can put together all the weights of our layer using a matrix: the weights of each neurons are the columns of the matrix. Since we have \(n\) weights for each neuron and \(m\) neurons in the layer the matrix will have \(n\) rows and \(m\) columns.

We can say that in a different way: each element of the matrix is in the form \(m_{ij}\), \(j\) indicates that we are dealing with the j-th neuron of the layer and \(i\) indicates that we are selecting the i-th weight of this neuron.

To summarize, our input is

$$ X = \left[ {\begin{array}{ccc} x_1 & \ldots & x_n \end{array} } \right] $$

and our weight matrix has the form

$$ W= \left[ {\begin{array}{cccc} w_{11} & w_{12} & \ldots & w_{1m} \\ w_{21} & w_{22} & \ldots & w_{2m} \\ \ldots & \ldots & \ldots & \ldots \\ w_{n1} & w_{n1} & \ldots & w_{nm} \end{array} } \right] $$

The dot product of this 2 matrices \(X \cdot W\) is an array with \(1 \) row and \(m\) columns. This simple matrices multiplication performs all the weighted sums for all the neurons of the layer. Now we have to take into account the biases. We have one bias for each neuron and so it natural to put them together into a matrix with \(1\) row an \(m\) columns

$$ b = \left[ {\begin{array}{ccc} b_1 & \ldots & b_m \end{array} } \right] $$

Let‘s forget for a moment the activation function (or we can suppose that the activation function is the identity function \(y(x)=x\)): the operation performed by the layer can be simply indicated with

$$ Y = X \cdot W + b $$

here we indicate the output with \(Y\) that will be a matrix with \(1\) row and \(m\) columns.

We can easily take into account also the activation function by indicating our function with \(f()\) and supposing that when it is applied to a matrix the function operates on each element of the matrix separately. At the end all the operations performed by a layer made by \(m\) neurons on an input array made by \(n\) items can be conveniently expressed in the form:

$$ Y = f( X \cdot W + b) $$

where \(f\) is the activation function (the same for each neuron, obviously). A Neural Network made by \(k\) layers is simply a sequence of \(k\) operations of this type.